Lugar geométrico de la linea recta
El lugar geométrico de los puntos que equidistan a otros dos puntos fijos y es una recta o eje de simetría de dichos dos puntos. Si los dos puntos son los dos extremos de un segmento , dicha recta, o lugar geométrico, es llamada mediatriz y es la recta que interseca perpendicularmente a en su punto medio.
Pendiente y Angulo de inclinación
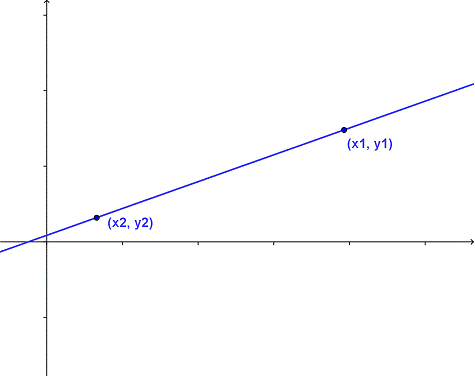
El ángulo de inclinación de una recta es el ángulo que forma con el eje x. La medida del ángulo se toma en sentido contrario a las agujas del reloj. ... La pendiente (GE/AE) es igual a la tangente del ángulo: m = tan h, o lo que es lo mismo 1/tan (o tangente elevado a -1) de la pendiente es igual al ángulo h.

Condiciones de Paralelismo y Perpendicularidad
Rectas paralelas
Dos rectas son paralelas si están de un mismo plano y no se intersectan, sin importar cuanto se prolonguen. Esta propiedad se representa con el símbolo.
Condición
Dos rectas ɩ₁ y ɩ₂ con pendiente definidas m₁ y m₂ son paralelas si tienen la misma pendiente; esto es, si m₁=m₂
Rectas perpendiculares
Dos rectas son perpendiculares cuando al intersecarse una con la otra forman cuatro ángulos de 90°
Condición
Dos rectas ɩ₁ y ɩ₂ con pendientes definidas m₁ y m₂ son perpendiculares si y sólo si m₁m₂ = -1
Esto es si sus pendientes son recíprocas y de signo contrario.
Ángulos entre dos Rectas
En el espacio, dos rectas pueden ser coincidentes, paralelas, secantes o bien cruzarse. ... Si dos rectas son coincidentes o paralelas forman un ángulo de . Si dos rectas son secantes, determinan cuatro ángulos iguales dos a dos. El menor de dichos ángulos se define como el ángulo entre las rectas.

FORMAS DE LA ECUACIÓN DE LA RECTA
PUNTO PENDIENTE
Un tipo de ecuación lineal es la forma punto-pendiente, la cual nos proporciona la pendiente de una recta y las coordenadas de un punto en ella. La forma punto-pendiente de una ecuación lineal se escribe como . En ésta ecuación, m es la pendiente y (x1, y1) son las coordenadas del punto.
Dos Puntos

Sean los puntos A (x1, y 1) y B (x2, y 2) que determinan una recta r. Un vector director de la recta es:

Cuyas componentes son:
Sustituyendo estos valores en la forma continua:

Ejemplos:
Hallar la ecuación de la recta que pasa por A(1,3) y B(2,-5)


Pendiente Ordenada al Origen
La gráfica de una ecuación en la forma pendiente-ordenada al origen. Para graficar una ecuación lineal dada en forma pendiente-ordenada al origen, podemos utilizar la información proporcionada por esa forma. Por ejemplo, y=2x+3 nos dice que la pendiente de la recta es 2 y la intersección con el eje y ocurre en (0,3).
SIMÉTRICA
ECUACIÓN SIMÉTRICA DE LA RECTA. La ecuación canónica o segmentaria de la recta es la expresión de la recta en función de los segmentos que ésta determina sobre los ejes de coordenadas. a es la abscisa en el origen de la recta. b es la ordenada en el origen de la recta.

GENERAL
La forma general de la ecuación de la recta es la que considera todos los casos de las rectas: horizontales, verticales e inclinadas. En otros casos no siempre es posible escribir la ecuación de una recta dada. Por ejemplo, en el caso de la ecuación de la recta en la forma simétrica, en caso de que cualquiera de las intersecciones fuera, bien  , bien
, bien  , la ecuación simétrica no puede escribirse.
, la ecuación simétrica no puede escribirse.
En el caso de la ecuación vertical, no puede escribirse ni en forma punto-pendiente, ni en forma pendiente-ordenada al origen. Esto se debe a que la recta vertical no tiene definida la pendiente. (¿Por qué?) Así que surge la necesidad de estudiar una clase más de forma de la recta.
Considera la ecuación de la recta en su forma simétrica:
Si multiplicamos ambos lados por  obtenemos:
obtenemos:
Ahora que hemos transformado la ecuación para evitarnos las fracciones, podemos cambiar los nombres de los coeficientes y escribir:
Esta es la ecuación de la recta en su forma general.
NORMAL
La pendiente de la recta normal a una curva en un punto es la opuesta de la inversa de la pendiente de la recta tangente, por ser rectas perpendiculares entre sí. Es decir, es la opuesta de la inversa de la derivada de la función en dicho punto.
Distancia de un Punto a un Recta
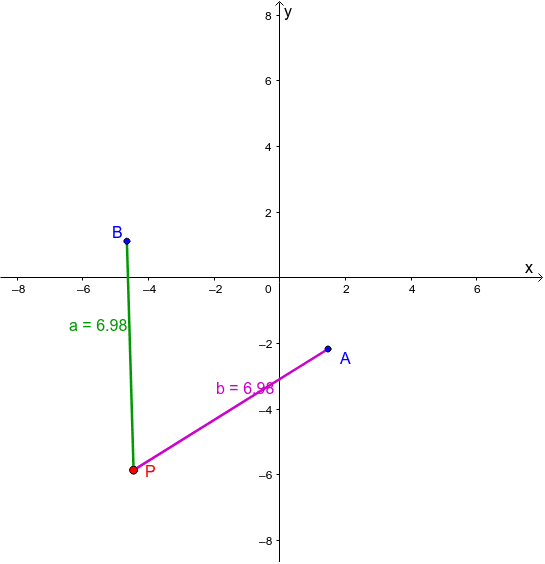
La distancia de un punto P1(x1; y1) a la recta r de ecuación Ax + By + C = 0, se denota por d (P1; r) y es calculada mediante una fórmula. Distancia de un punto a una recta. Al calcular la distancia de un punto P1 a una recta r, se determina la longitud del segmento perpendicular que une al punto P1 con la recta r
 y
y
No hay comentarios:
Publicar un comentario